
I hope this replies to your question and helped you. Using such techniques you can prove everything, well at least for everything I tried to prove, I was able to.

Let $G$ be a Lie group with Lie algebra $\mathfrak$ we obtain the wanted formulas. We can use the exponential map between the Lie algebra and the Lie group to provide a rigorous definition of sine and cosine. To cut a long story short: Can be done and has it been done by someone? A purely geometrical yet rigorous definition of sine and cosine or can it proved that it's doomed to fail as the circular dependencies can't be avoided? The usual way to introduce the arc length would require me to know the derivate of sine and cosine but using that is prohibitive here as we have not yet defined sine and cosine. When you try to prove the five "axioms" then all difficulties are related to the arc length.
#COSINE GEOMETRY DEFINITION SERIES#
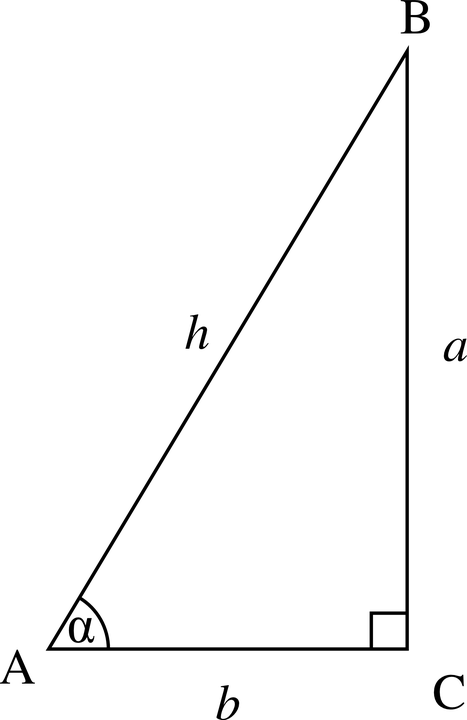
In other words, if a pair of functions are subject to the five axioms, they are the sine and the cosine.Įventually, the introduce the well-known power series for both sine and cosine and show that they abide to the axioms and hence we know, they are the sine and the cosine. They then state that these five axioms already uniquely define a pair of functions. They would abide to the respective addition formulas. Sine is an odd and cosine an even function. Sine and cosine are defined on the real domain and are continuous. Then they said, the following properties could (in theory) be proved but to avoid the above mentioned challenges, they'd rather introduce them as axioms: The explicitly mentioned that these definitions were dependent on arc length, whose definition they would omit here though but rather rely on intuition. They gave us the intuitive definition of sine and cosine using the unit circle. It is the longest side in a right triangle. The hypotenuse of a right triangle is always the side opposite the right angle. We use special words to describe the sides of right triangles. One of my beginners courses at the university for example did like that: In a right triangle, the hypotenuse is the longest side, an 'opposite' side is the one across from a given angle, and an 'adjacent' side is next to a given angle. The question is: Is it possible to give a rigorous definition of sine and cosine not using the power series approach? I'd like to revisit a question that has been brought up a couple of times here on math.stackexchange, yet as far as I'm aware, nobody has come up with a final answer.


 0 kommentar(er)
0 kommentar(er)
